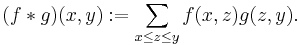Locally finite poset

In mathematics, a locally finite poset is a partially ordered set P such that for all x, y ∈ P, the interval [x, y] consists of finitely many elements.

Given a locally finite poset P we can define its incidence algebra. Elements of the incidence algebra are functions ƒ that assign to each interval [x, y] of P a real number ƒ(x, y). These functions form an associative algebra with a product defined by

$(f * g)(x,y):=\sum_{x \leq z \leq y} f(x,z) g(z,y).$

(See incidence algebra for more details)

In theoretical physics a locally finite poset is also called a causal set and has been used as a model for spacetime.

References

Stanley, Richard P. Enumerative Combinatorics, Volume I. Cambridge University Press, 1997. Pages 98, 113—116.